
ritim gitar ders notları
Tarih boyunca pek çok matematikçi müzikle ilgilenmiştir. Bazılarımızın aklına ‘Acaba pek çok müzisyen de matematikle ilgilenmiş midir?’ gibi bir soru takılabilir. Kuşkusuz ilgilenen müzisyenler vardır ancak bir karşılaştırma yapılırsa matematikçiler çok daha öndedirler.
Eski Yunan’ da müzik, matematiğin 4 ana dalından biri olarak kabul edilmiştir. Pythagoras (M.Ö. 586) okulunun (Quadrivium) programına göre Müzik; Aritmetik, Geometri ve Astronomi ile aynı düzeyde kabul görmüştür.
Bir telin değişik boyları ile değişik sesler elde edildiğini ortaya çıkartan Pyhagoras, M.Ö. 6. yüzyılda yaşamıştır ve bugün kullanılmakta olan müzikal dizinin temelini oluşturması açısından oldukça önemli bir iş yapmıştır.
Pythagoras, 12 birimlik bir teli ikiye bölmüş ve oktavı elde etmiştir. Elde edilen 6 birimlik uzunluk ( telin ½ si), 12 birimlik uzunluğun bir oktav tizidir. Pythagoras 8 birimlik uzunluk ile (telin 2/3 ü) 5 li aralığı, 9 birimlik uzunluk ile (telin ¾ ü) 4 lü aralığı bulmuştur.
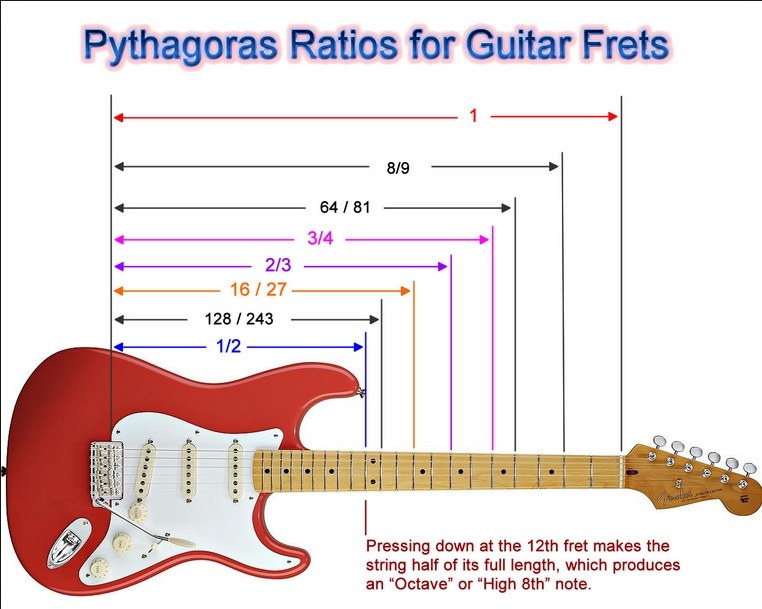
Pythagoras oranlarına göre, 5 li ile 4 lü arasındaki fark tam tonu vermektedir.
2/3:3/4=8/9 (5T-4T=2M ) Yani, tam sesin 8/9 ile çarpımı bize o sesin bir ton tizini vermektedir.
Devam edecek olursak; 8/9.8/9=64/81 (2M+2M=3M)
Esas sesimiz “do” olsun. Do nun ½ si bize do nun bir oktav tizini, 2/3 ü “sol” sesini, ¾ ü “fa” sesini, 8/9 i ise “re” sesini, 64/81 i ise ” mi” sesini vermektedir.
Bu şekilde gidildiği zaman; Do, re, mi, fa, sol, la, si, do sesleri sırasıyla; 1, 8/9, 64/81, ¾, 2/3, 16/27, 128/243 ve 1/2 oranları ile ifade edilir.
Pythagoras, telin 8/9 u ile 1 tam tonu elde etmiştir, ancak bir notaya 6 kez tam ton ilave edildiğinde neredeyse o notanın oktavı elde edilmiştir ki bu da “Pythagoras koması” olarak adlandırılır. Bu durumda Pythagoras sisteminde bazı değişikliklere gerek duyulmuş ve böylece zaman içinde tampere edilmiş bir şekilde 12 eşit yarım tonluk bir sistem geliştirilmiştir. 1 tam ton 8/9 ile değil iki yarım ton ile gösterilmiştir.
Aşağıdaki animasyonda rakamları tıklayarak olayı daha iyi gözlemleyebilirsiniz.
Kaynak: https://www.matematiksel.org/muzigin-icindeki-matematik-matematigin-icindeki-muzik/









Müzikteki matematiksel gizemi keşfederek yazıya dökmenin ilk temeli Pisagor (Pythagoras, M.Ö. 530-450) tarafından atılmıştır. Biz kendisini okul sıralarından o meşhur dik üçgen teoremi ile hatırlarız ama Pisagor günümüzde ulaştığımız bilim seviyesinin babasıdır. O kendi devrine kadar gelişmiş bütün çalışmaları bir disiplin altında toplamış, geometri, aritmetik, astronomi, coğrafya, müzik ve tabiat bilgisi olarak ayrı ayrı bilim dalları yaratmıştır.
Pisagor bilimi, bilim için düşünüyor, bilimin uygulamaları onu ilgilendirmiyordu. Bu nedenle ‘bilgi seven’ anlamındaki ‘filozof sözcüğünü ilk olarak o kullanmıştır. Pisagor tüm evrenin sayılar ve aralarındaki ilişkilere göre kurulduğuna inanıyordu.
Pisagor’un müziğin içindeki matematiği bir demirci dükkanının önünden geçerken keşfettiği rivayet edilir. Demirci ustasının, demir döverken kullandığı aletlere göre değişik sesler çıkarması Pisagor’un ilgisini çekmiş, dükkanı kapattırarak ustaya çeşitli aletler kullandırmış, çıkan sesleri incelemiş ve kayıtlar almış.
Batı müziği 9. yüzyılın başına kadar notalamadan habersizdi. Eserler kulak yoluyla kuşaktan kuşağa aktarılıyor, bu arada değişime uğruyor, zamanla unutulabiliyordu. 9. yüzyılın ikinci yarısında ilk notalama sistemi ortaya çıktı. Arezzo’lu Guido’nun (Gui d’Arezzo) notalama sisteminin seslerin yüksekliğini kesin olarak belirtmeye başlamasıyla büyük bir ilerleme kaydedildi. 11. yüzyılda notaların üzerine dizildiği beş çizgiden oluşan “porte”nin kullanılmasıyla notaların yüksekliği (do, re, mi,….) ve süresi (birlik, ikilik, dörtlük,….) kesin biçimde belirlenebilir hale geldi.
Aslında müziğin dört parametresi vardır: Yükseklik, süre, şiddet ve tını. Bunlardan ilk ikisi zamanla genel kabul gören bir takım işaretler sayesinde kağıt üzerine dökülebilmiş, şiddet ve tını ise notanın yanında ek kelimelerle belirtilmişler ve kısmen de yoruma açık bırakılmışlardır.
Çeşitli sesleri belirtmek ve bunların birbirlerine karışmasını önlemek için sesleri temsil eden notalara özel isimler verildi. Do, re, mi, fa, sol, la, si. İngilizce’de ve Almanca’da ise notalar harflerle gösterildi(C=do, D=re, E=mi, F=fa, G=sol, A=la, B=si-ing.-, H=si-alm.-).
Nota isimlerinden ‘do’nun önceki ismi ‘ut’ idi. Sesli harfle başlayan bu isim, notaları sırayla söylerken tutukluk yaptırdığından 12. yüzyılda ‘do’ olarak değiştirildi. Almanya ve bazı ülkelerde ‘ut’ hala kullanılır.
‘Si’ hariç diğer notaların isim babası Gui d’Arezzo’dur. Arezzo bu adları Aziz lohannes Battista ilahesindeki mısraların birinci hecelerinden alarak takmıştır. Yedinci notanın adı uzun zaman ‘B’ olarak kalmış, sonradan 13. yüzyılda Sanete lohannes kelimelerinin baş harflerinden meydana gelen ‘si’ adını almıştır.
Notalamanın keşfi ve gelişimi müzik pratiğine olağanüstü bir gelişme ortamı yaratmıştır. Notalama, icracıyı ezberden kurtararak hem müzik parçalarının uzamasına hem de çeşitli dönemlere ve ülkelere ait notalanmış eserlerin katılmasıyla repertuarın zenginleşmesine ve çeşitlenmesine imkan vermiştir. Nota sayesinde bir müzisyen bilmediği bir müzik parçasını icra edebilmek için tek başına yeterli bir hale gelmiştir.
Tamer Korugan / Lüzumsuz Bilgiler Ansiklopedisi 2