
klasik müzik
Bu zamana dek çok sık işittiğimiz bir söz vardır müzikle ilgili. Onu ‘ruhun gıdası’ olarak tanımlarlar. Ancak gün geçtikçe müziğin işlevinin sadece ruhsal gelişimde değil aynı zamanda beyin gelişiminde de ana rolü üstlenebileceği görülüyor. Bu özellikle klasik müzik için birçok deneyle tespit edilebilen bir durum haline geldi.
Rönesans Dönemi’nde(1450-1600) müziğin gelişimi çok sesliliğe doğru evrildi. Kilise çevresinde gelişmeye başlayan çok sesli müzik anlayışı, İtalyan kutsal müzik bestecisi ve Roma Ekolü’nün baş temsilcilerinden Giovanni Pierluigi da Palestrina ile zirveye ulaştı. (1525-1594).
Peki matematik ile klasik müzik nasıl kesişiyor?
Son araştırmalar klasik müzik ile matematik arasında temel bağlantılar bulunduğuna dikkat çekiyor. Öğrenme kapasitesini artırdığı gözlenen klasik müziğin matematiksel yapısı ile beynin alfa dalgaları uyarılıyor ve ilginçtir ki fiziken temel ihtiyaçlara eriştiğimiz zaman -karın doyurmak gibi- beynin uyarılmasını tetikleyen durumlardan daha etkili olduğu gözlemleniyor.
Yani doyma hazzından gelen geçici etkiye kıyasla ele alınırsa beyine ‘kalıcı’ uyarılar yapan işleve sahip.
Peki bu kalıcı etkiyi sağlayan klasik müziğin oluşumunda matematiğin gözlemlenmesi mümkün mü? Gerçekten de Leibniz’in dediği gibi ‘müzik ruhun gizli bir matematiksel problemidir’ çıkarımı yapılabilir mi? Eski Yunan okullarından Quadrivium neden müziği astronomi, geometri gibi diğer bilimlerle eş tutmuştur? Kısa bir inceleme yapalım:
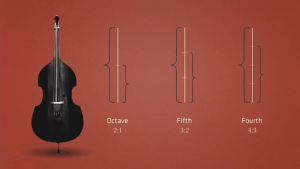
PYTHAGORAS ARALIKLARI
Tek sesliden çok sesliye geçiş niteliğindeki klasik müziğin bu yapısı Pythagoras’ca(MÖ 6.yy) daha görülür bir biçime sokulmuştur. Tetrakord prensibince –dört sesin bir arada duyulması- temel atmış ve oktav tizlerinin incelemiştir. 6,8,9,12 sayıları tetrakordun temel sayılarıdır ve 6 br bir oktav tizi olarak tanımlanmıştır. (12 br lik bir telin yarısından elde edilmiş). 8 br için (telin 2/3’ü) 5’li aralığı, 9 br için 4’lü aralığı bulmuş ve literatüre çok önemli bir temel eklemiştir.
[xt_go_advt_3]PEKİ OKULLARDA GÖZLENEBİLEN ETKİ NEDİR?
Okullarda nitelikli şekilde verilecek müzik eğitiminin matematik eğitiminden önce verilmesinin, beyinde matematiksel bir yapı inşasında temeli sağlamlaştıracak bir yapıtaşı olduğu düşünülmektedir. Uzaysal zekayı geliştirecek kalıcı beyin gelişiminin klasik müzikle sağlanabileceği ve matematiğin temellerinin bu müzikal disiplin sonrasında doğal olarak ve güçlü bir şekilde ortaya çıkacağı düşünülmekte, daha doğrusu gözlemlenmektedir.
Gözlem ‘MOZART ETKİSİ’ne(Mozart Effect) dayanır. Mozart’ın müziğinde ‘altın oran’ olduğu düşünülüyor ve bu düşünceler O’nun müziğini dahice ve sayısal olarak niteleyen yorumlar baz alınarak deneylerde kullanılıyor.
Mozart Etkisi için gözlemsel çalışmalarda, fareler ve labirent bağıntısı kullanıldı. Labirent çözme kabiliyetinin, farelere uzun süre Mozart müziği dinlettirilmesi ile çok daha başarılı ve kalıcı sonuçlar verdiği gözlemlenmiştir.
Görülüyor ki klasik müzik ve matematik arasında azımsanamayacak bir doğrudan ilişki var. Eğitim sisteminde daha kalıcı sonuçlar elde edebilmek için klasik müzik kültürünü yaygınlaştırmak daha etkili sonuçlar verebilir. Klasik müziğin matematiksel yapısı, Galileo’nun matematiği tüm bilimlerin ortak dili olarak nitelemesi gün geçtikçe ne kadar doğru bir tanımlama olduğunu göstermektedir. Siz de, altın oran ile oluşturulduğu düşünülen eserlerden George Frideric Handel’in ‘Hallelujah’ adlı eserini dinleyip kısa bir gözlem yapabilirsiniz.
Kaynak : Ceren Demir – Matematiksel.org








